前半の補足です。前半で紹介したシミュレータ云々について。
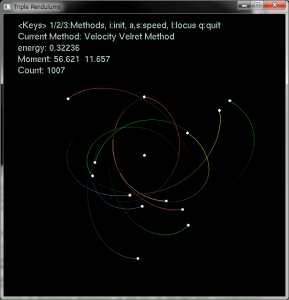
この粒子の振る舞いについて
「なんで星の運動を模してるのに楕円軌道じゃないんだ?」と思った方はとても勘のいい方です。
これは2次元の運動をどう考えるかによるものです。
3次元空間の平面上に粒子を配置させて運動させた場合、重力は距離の2乗に反比例しますが、
3次元空間に無限長の棒を(平行に)置いて運動させた場合、重力は距離の1乗に反比例します。
これはまあ真面目に積分してもそうなりますし、電磁気学を勉強したことのある方は雰囲気で理解できるかと思います。後者は宇宙空間では仮定が不自然すぎるだろうと思われるかもしれませんが、万有引力が3次元空間で逆2乗の法則に従っているとするなら、2次元では逆1乗になるのが自然だとも考えられます。
まあ、今回はそこまで哲学的な話ではなく、単に逆1乗のほうが見栄えが良かったからです。
どう見栄えに影響するかですが、これは無限遠点での挙動の違いを考えればだいたいわかります。位置エネルギーは力の積分(の-1倍)で与えられますが、これより力が逆2乗、逆1乗の場合のそれぞれについて位置エネルギーは逆1乗、logとなります。つまり前者ならエネルギーが無限遠である値に収束するのに対して、逆1乗なら際限なく増えていきます。
つまり、逆2乗ではひとたび粒子が第三宇宙速度に達してしまうと二度と戻ってこないのに対し、逆1乗なら少なくともいずれは引き戻されてくるという大きな違いがあります。見た目に粒子がどこかに飛んでいってしまうのは寂しいですね。
よく「この世が2次元だったらいいのに」という言葉を聞きますが、そんなことをしたら、上記の理由から世界中のものがある一点に集まってしまってつまらない世界になるだろうなあと思っています。
なお、粒子があまり近づきすぎると計算上の問題からヤバいことが起きるので、引力を打ち消すだけの反発力を与えてあります。
現実だと衝突しますが、無理にエネルギーを保存させようとして星が完全弾性衝突をするのもあまりリアリティがないですね。
これは速度ベルレ法の適用範囲に限界があるからです。(下は剛体3重振り子の動画)
シンプレクティック法は、影のハミルトニアンと呼ばれる量を厳密に保存する運動を記述します。この際、位置 を計算する際に
を計算する際に のときのハミルトニアン(の偏微分)が必要になります。これは普通に考えると右辺と左辺がからまってさくっと解けません。
のときのハミルトニアン(の偏微分)が必要になります。これは普通に考えると右辺と左辺がからまってさくっと解けません。
しかし都合のいいことに、単純な場合ハミルトニアンHは位置qと運動量pの足し算に分離でき、このときハミルトニアンの偏微分の形からqがなくなります。その場合の解法のひとつが速度ベルレ法となるわけです。
以前の3重振り子では、ハミルトニアン(というよりラグランジアン)の計算に3つのθという一般化座標を使っていました。このためハミルトニアンの分離が行えなくなり、(実際にはできるかもしれないけど私はその数学を持ち合わせていないので、)速度ベルレ法をはじめとした陽解法が使えない状態に陥っていました。
こういった場合には陰解法のガウス・ルジャンドル法などを使って解くことができます。
なんとなく当然のような気もしますが、よくよく考えてみるとこの仮定は結構不思議なことです。分子動力学法などではたいていこの仮定が成り立ってしまいます。
ソースコード
ちょっとだけかいつまんで書いておきます。C++です。
まずは系の状態の定義。数値積分に関しては位置と速度のペアのリストさえあればいいのだけど、肝心な力の計算ではどの値がどの物理量に対応しているかを知らなければならず、もどかしい。
かといって値を参照して保持しておくほどの大げさなものでもない。そこで、どうせ数値積分では四則演算くらいしか使わないので、粒子のvectorに必要な演算子のみ定義した構造体を持っておきます。
struct partState{
double x, y;
double vx, vy;
partState() : x(0.0), y(0.0), vx(0.0), vy(0.0){}
partState(double _x, double _y, double _vx, double _vy)
: x(_x), y(_y), vx(_vx), vy(_vy)
{}
};
struct partSystem{
std::vector<partState> pss;
partSystem(int size){
pss = std::vector<partState>(size);
}
};
const partState operator+(const partState& lhs, const partState& rhs);
const partState operator-(const partState& lhs, const partState& rhs);
const partSystem operator+(const partSystem& lhs, const partSystem& rhs);
const partSystem operator-(const partSystem& lhs, const partSystem& rhs);
const partState operator*(const double lhs, const partState& rhs);
const partSystem operator*(const double lhs, const partSystem& rhs);
力の計算はもうほんとに全ペアで単純に逆1乗で計算してるだけで、高速化のかけらもありません。
ガチで分子動力学法などをやるときには今回のO(n^2)のようにならない工夫が必要です。
partSystem calcForce(const partSystem& _ps){
partSystem ans(size);
for(int i = 0; i < size; i++){
for(int j = i+1; j < size; j++){
double dx = _ps.pss.at(i).x - _ps.pss.at(j).x, dy = _ps.pss.at(i).y - _ps.pss.at(j).y;
double r2 = dx*dx + dy*dy;
double r = std::sqrt(r2);
if(r > r_threshold){
//double r12_e3 = r2/0.0001;
//r12_e3 = r12_e3*r12_e3*r12_e3*r12_e3*r12_e3*r12_e3;
double f = -g*masses.at(i)*masses.at(j)/r;// + g2*masses.at(i)*masses.at(j)/r12_e3;
double fx = f*dx/r, fy = f*dy/r;
ans.pss.at(i).vx += fx;
ans.pss.at(i).vy += fy;
ans.pss.at(j).vx -= fx;
ans.pss.at(j).vy -= fy;
}
}
ans.pss.at(i).x = _ps.pss.at(i).vx;
ans.pss.at(i).y = _ps.pss.at(i).vy;
}
return ans;
}
反発力を与える際、分子動力学チックに高次の多項式の反発力を与えようとした名残があります。結局そこまでする必要もなく削除。かわりに距離にしきい値を導入します。
エネルギーの計算(表示用)でも不整合がないようにしておく必要があります。
あとは今回のテーマだった数値積分。ソースはとっても単純。
void move_euler(const double dt){
auto psDiff = calcAccel(ps);
ps = ps + dt * psDiff;
}
void move_heun(const double dt){
auto k1 = calcAccel(ps);
auto k2 = calcAccel(ps + dt*k1);
ps = ps + dt/2.0*(k1+k2);
}
void move_runge_kutta(const double dt){
auto k1 = calcAccel(ps);
auto k2 = calcAccel(ps + dt/2.0*k1);
auto k3 = calcAccel(ps + dt/2.0*k2);
auto k4 = calcAccel(ps + dt*k3);
ps = ps + dt/6.0*(k1+2*k2+2*k3+k4);
}
void move_velocity_velret(const double dt){
auto k1 = calcAccel(ps);
auto p2 = ps;
for(int i = 0; i < size; i++){
p2.pss.at(i).x += dt*ps.pss.at(i).vx + dt*dt/2.0*k1.pss.at(i).vx;
p2.pss.at(i).y += dt*ps.pss.at(i).vy + dt*dt/2.0*k1.pss.at(i).vy;
}
auto k2 = calcAccel(p2);
for(int i = 0; i < size; i++){
p2.pss.at(i).vx += dt/2.0*(k2.pss.at(i).vx + k1.pss.at(i).vx);
p2.pss.at(i).vy += dt/2.0*(k2.pss.at(i).vy + k1.pss.at(i).vy);
}
ps = p2;
}
速度ベルレ法だけ、位置と速度を明示的に扱っているのがわかります。