知性は、方法や道具に対しては鋭い鑑識眼を持っていますが、目的や価値については盲目です。 – アインシュタイン
大学院の夏学期の授業で自由課題が出たのですが,その提出物を授業で発表することになりました.
課題で愉快な結果が出たわけでもないのですが,せっかくなのでそのとき作ったプログラムとその結果を書き留めておきます.
テーマは「モンテカルロ法」.何か身近な問題についてシミュレーションを行ってこいとのことでした.
モンテカルロ法は乱択アルゴリズムの一種です.ざっくり言ってしまえばたくさんやってみて統計をとるという方法ですね.
コンピュータのくせに「答えは厳密ではないが,たぶんだいたい合ってる」という結果の出方が大好きです.
さて,たくさんのものをぼんやり見る…となるとやはり気になるのは人の群れのシミュレーションです.人って群れると不思議な振る舞いをしますよね.
研究となると面倒な分野ですが,授業の課題なら気にせず変なことができます.
それで扱う現象ですが,人って誰かの隣には座らないんですよね.電車などに乗っているとよく見る景色です.
これは映画館とか大学の講義でも同じで,隣が開いてる席があったらそっちを使うというのが人間というものの性質のようです.
男子トイレでも同じことが起きますね.大きなトイレでがら空きなら誰かの隣の便器というのは普通使いません.もしがらがらのトイレで隣に人がやってきたら,何か他の目的があるのではという考えが頭をよぎります.
で,あのふるまいのシミュレーションをしてみようと思ったわけです.
トイレのモデルは以下のようになります.
便器の数をn個として,そこに人が次々と到着します.各個人の便器使用時間はガウス分布,到着時間はポアソン到着としています.
各個人は両隣が空いている便器があればそれを,なければそれ以外の便器を使います.全部埋まっていたら待ち行列に並びます.待ち行列の人は便器が空き次第詰めていきます.
同程度の魅力の便器があればランダムに選びます.
パラメータは便器数n, 便器使用時間の平均μおよび標準偏差σ,それと平均到着時間間隔λとなります.
便器使用時間についてはどこかにデータがあればよかったのですが,見つからなかったので自分で1週間計測しました.
平均は20秒,標準偏差は3秒となりました.今回は両側に3秒追加して26±3秒としてシミュレーションを行いました.
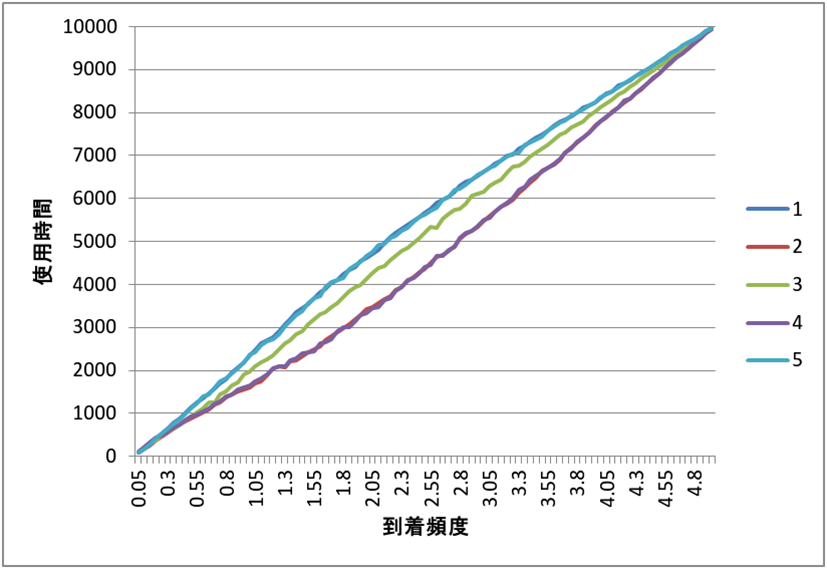
n=5として平均到着時間間隔λを変化させた結果が以下になります.右の番号はトイレの便器ですね.端から順に1から5です.
横軸は到着頻度(λ)になります.左端は人が来ない状況で,右に行くにつれてトイレが賑わっていきます.右端は常にトイレが使われているという相当やばい状態ですね.現実にこんなトイレがあったら早いところ増設したほうが事故を未然に防げていいと思います.
人がとてもまばらな時は,どの便器も同様に使われます.また相当混んでいる時も同様に使われます.
まあ他人がいなければ区別なく使いますし,混んでる時は選ぶ余地もなく全部使われてるので当然とも言えます.
問題はこの中間のときで,ちょうど限界の半分くらいの人が押し寄せるときに便器の使用頻度に差が生じます.
端のトイレが比較的よく使われる一方で,端から2番目のトイレ(2,4)の使用頻度は落ちています.おそらく端っこは隣が片方しかないため,そこそこ混んでいても入りやすいのだと思います.それでその隣は使われないのでしょうね.
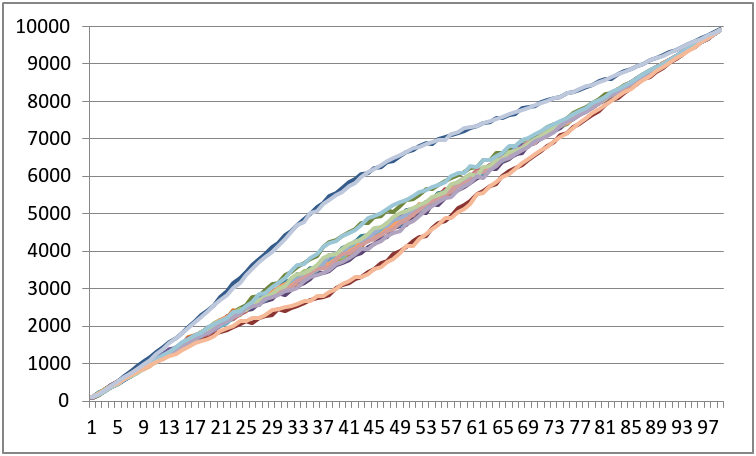
以下が便器の数n=31とした結果です.大きなトイレですね.
多くの便器達はおおよそグラフの中央に集まっています.これは便器ごとに使用率が変わらないことを意味しています.
一方で上に大きく曲がった線が2本あります.これが両端の便器です.使用率は他のものに対して有意に高くなっています.
下の2本は端から2番目の便器になります.こちらは使われにくくなっていますね.
現実問題を表現できていますかね?
今度駅とかのトイレに行ったときは便器の使用状況に気をつけてみるのもいいかもしれません.
この結果から何がわかるか?というと,まあせいぜい端の便器は汚れてるかもしれないよ,ということくらいです.
まあトイレに限らずなんでもそうかもしれません.大学の教室の椅子でも5席あったら1,5番目,詰まったらその後3番目から埋まりますね.
これ自体は非常に単純なシミュレーションですが,簡単な仮定をおくだけでこのようなデータが得られるのがシミュレーションの面白いところです.
気軽にコードが書けるとこういった遊びの幅も広がります.
コメントも書いてないものですが一応ソースコードを置いておきます.Visual Studio 2010で作ったものですが単純なC++のコードなのでだいたいの環境で動くと思います.
発表に使った資料も置いておきます.後半は違う話になっていますがいずれここで書けたら面白いかなと思っています.
シミュレーションの内容に補足をすると,今回はキネティックモンテカルロ法という手法になっています.これは扱う時間のスケールに対して稀な現象を含めて扱うときに使われる手法のひとつで,系で起きるイベントをリストアップし,次のイベントまでにかかる時間を計算してイベント単位で時間を進めていく方法です.
また,このコードにはトイレの待ち行列が伸びすぎるとクラッシュする機能があります.シミュレーションとはいえあんまり我慢させるのはかわいそうですから.
ちなみにトイレシミュレータの原案は昨年の研究室の先輩方でした.先輩方ありがとうございました.