別にプリクラに貪欲なわけではありません。
あのね。前々からずーーっと答えが知りたい数学の問題があって。 ①n人のグループがいる ②プリクラ機には一度にm人しか入れない メンバーがほかの各メンバーと一度は同じ写真におさまるためには最低何回撮影する必要があるか? ※ちなみに(n,m)=(7,5)の時は3 #プリクラ問題
— あしやまひろこ (@hiroko_TB) January 1, 2015
こちらの問題にまつわる話です。
下限については比較的よいものがすぐ求まるのですが、理論解となると私の知識では太刀打ち出来なさそうだと思いました。
困ったときにはコンピュータ。理論解ではありませんが、それらしい方針を与えて近似解を求めてもらおうという魂胆です。
ソースコードは一番下へどうぞ。正直な話、今回はソースをはりつけるために作られた記事です。
まずは問題の整理。n人がすべての他人とつながるようにm人ずつ切り分けていく問題です。
言い換えると、接点がn個あり全てがつながっている完全グラフについて、接点数mの部分完全グラフ(クリーク)の集合で 全ての辺を被覆する問題ということができます。
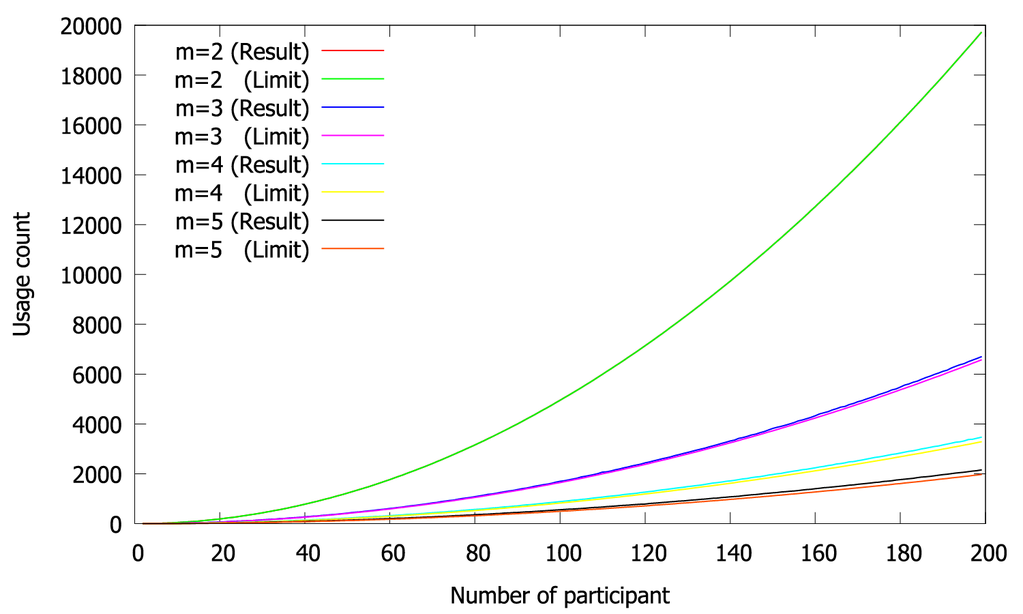
全体の辺の数は組み合わせの表記でnC2個あり、接点数mの部分グラフではmC2個あるため、ここから下限値を求めることができます。
ただ、ここから先が問題。実際にnC2/mC2個の部分グラフで全体を覆うためには全く無駄のない選び方をする必要があるのですが、これができるのかどうかがよくわかりません。できる場合もたまにあります。(n=7,m=3など。どうやらm=3のときは、nが2^x-1の形のとき無駄なく選べるようです。)また明らかにできない場合もあります。(n-1がm-1で割れないとき。ある個人から見てどうm人ずつ組んでも余りが出ます。)というわけで、ここから先はなんとも全体像を掴みにくい世界になっていきます。
そこでコンピュータの出番です。今回は完全グラフの問題ということで、ネットワークが濃すぎて分割統治法にも動的計画法にもつなげられなかったので、貪欲法で近似解を解くことにします。
グループを作るルールとしては、残り相手の最も少ない人を1人目として、そこから「グループのメンバー全体と最もつながりが少ない人」を探して順にグループに入れていきます。つながりの少ない人がたくさんいた場合には残り相手の少ない人を優先します。このルールで順番にグループを作っていきます。
どうやら、ほとんど無駄なくグループを組むことは可能なようです。グループ分けの実際の区切りを知りたい方は、下のソースコードをいじって調べてみてください。
ここから先はソースコードです。言語はC++11で書かれています。
#include <cmath>
#include <iostream>
#include <vector>
#include <algorithm>
class graph_mat{
std::vector<std::vector<char> > mat;
std::vector<int> node_left;
const std::vector<char> connected_node_sample;
int msize;
public:
graph_mat(int n) : msize(n), connected_node_sample(n, 1){
mat.resize(n);
node_left.resize(n);
for(int i = 0; i < n; i++){
mat[i] = std::vector<char>(n,0);
mat[i][i] = 1;
node_left[i] = n-1;
}
}
int size() const{ return msize; }
bool connected(int i, int j) const{
return mat[i][j]==1;
}
int min_empty_node() const{
int ans = size();
for(int i = 0; i < mat.size(); i++){
if(node_left[i] != 0){
ans = i;
break;
}
}
return ans;
}
int node_left_edges(int node) const{
return node_left[node];
}
void connect(int i, int j){
if(!connected(i, j)){
node_left[i] -= 1;
node_left[j] -= 1;
}
mat[i][j] = 1;
mat[j][i] = 1;
}
void add_group(const std::vector<int>& nodes){
for(int i = 0; i < nodes.size(); i++){
for(int j = i+1; j < nodes.size(); j++){
connect(nodes[i], nodes[j]);
}
}
}
};
int connect_num(const graph_mat& g, const std::vector<int>& nodes, int nnode){
int ans = 0;
for(auto it = nodes.cbegin(); it != nodes.cend(); ++it){
if(g.connected(*it, nnode)) ans++;
}
return ans;
}
int min_connect_node(const graph_mat& g, const std::vector<int>& nodes){
int min_node = g.size();
int min_connect = nodes.size();
int min_left_node = g.size();
for(int i = 0; i < g.size(); i++){
if(find(nodes.begin(), nodes.end(), i) != nodes.end()) continue;
int connect = connect_num(g, nodes, i);
int left_node = g.node_left_edges(i);
if(connect < min_connect || (connect == min_connect && left_node < min_left_node)){
min_node = i;
min_connect = connect;
min_left_node = left_node;
}
}
return min_node;
}
std::vector<int> new_group(const graph_mat& g, const int group_num){
std::vector<int> ans;
int min_left_edge = g.size();
int min_node = g.size();
for(int i = 0; i < g.size(); i++){
int left_edge = g.node_left_edges(i);
if(left_edge != 0 && left_edge < min_left_edge){
min_node = i;
min_left_edge = left_edge;
}
}
//ans.push_back(g.min_empty_node());
ans.push_back(min_node);
while(ans.size() < group_num){
int next_node = min_connect_node(g, ans);
if(next_node == g.size()) break;
ans.push_back(next_node);
}
return ans;
}
int group_count(const int total, const int group_num){
graph_mat g(total);
std::vector<std::vector<int>> groupes;
while(g.min_empty_node() != g.size()){
auto group = new_group(g, group_num);
groupes.push_back(group);
g.add_group(group);
/*
for(auto it = group.begin(); it != group.end(); ++it){
std::cout << *it << " ";
}
std::cout << std::endl;
*/
}
return groupes.size();
}
int main(int argc, char** argv){
for(int i = 2; i < 200; i++){
std::cout << i;
for(int j = 2; j < 7; j++){
int lower_bound = std::ceil((1.0*i*(i-1))/(1.0*j*(j-1)));
int gnum = group_count(i, j);
std::cout << ", " << lower_bound << ", " << gnum;
}
std::cout << std::endl;
}
return 0;
}