別にプリクラに貪欲なわけではありません。
あのね。前々からずーーっと答えが知りたい数学の問題があって。 ①n人のグループがいる ②プリクラ機には一度にm人しか入れない メンバーがほかの各メンバーと一度は同じ写真におさまるためには最低何回撮影する必要があるか？ ※ちなみに(n,m)=(7,5)の時は3 #プリクラ問題
— あしやまひろこ (@hiroko_TB) January 1, 2015
こちらの問題にまつわる話です。
下限については比較的よいものがすぐ求まるのですが、理論解となると私の知識では太刀打ち出来なさそうだと思いました。
困ったときにはコンピュータ。理論解ではありませんが、それらしい方針を与えて近似解を求めてもらおうという魂胆です。
ソースコードは一番下へどうぞ。正直な話、今回はソースをはりつけるために作られた記事です。
招き猫
選挙シーズンですね。
選挙といえばお馴染みのテレビの開票速報。20時を過ぎた瞬間から「ほんとに確実なのかよ、というか1票でも確認したのかよ」と言いたくなるペースで大物政治家の当確報道が流れていくのが恒例行事です。
まあそう言って報道につっかかるのも野暮というもので、単に確実という言葉が100%でなくだいたい正しいという意味で使われているだけですね。(個人的には票を見ずに結果を宣言するのはなんとなく投票という行為自体を軽く扱っている気がするのですが、それはまた別の話。)
結局のところ、どういう理屈で当確が出ているのかは視聴者にはわからずじまいなわけです。出口調査や前回までの結果など複雑なノウハウが詰まったものだし簡単に教えてくれるものではないでしょうが、このご時世、「なんかいろいろやってるんだよ、まあ信じておきな」ではどうにもしっくりこないところがあります。
そこで今回は視点を変えて、「逆に票だけを見て確率的に『確実』というためには、全体のうちのはじめの何票くらいを集計すればいいのか」というのを試しに計算してみたいと思います。
やっていることは二項分布のベイズ推定をしているのみで、数学的にはゆったりした話かと思います。
(以下、なるべく政治的な話にならないよう、具体例では実名を挙げないように気をつけます。)
先日のマンデルブロー集合の10の200乗倍で作成したプログラムがあるので、今回はマンデルブロー集合の様々な地点へ飛び込んだ動画を作ってみました。
前回の記事を見ていない方はそちらからどうぞ:
今回訪れる地点は計5箇所です。どの点も拡大していく最中に集合全体と同じ形が現れます。フラクタルらしくて面白いと思います。
具体的には以下の点です。緑は前回の場所。それぞれ個性的な場所だと思います。
Mandelbrot Set with Circles (from Wikimedia)
この集合はフラクタルなので自己相似の図形ではあるのですが、ただ単純にどこでも同じ形を持っているわけではありません。拡大する場所を変えると景色が一変してしまいます。
肝心の動画はこちら。ニコニコ動画はこちら。
今回の話題はこれです。
ジョーカーを除いたトランプ５２枚の中から１枚のカードを抜き出し、
表を見ないで箱の中にしまった。
そして、残りのカードをよく切ってから３枚抜き出したところ、
３枚ともダイヤであった。
このとき、箱の中のカードがダイヤである確率はいくらか。
答えが１／４ってのは納得出来ない！
１０／４９だろ！！
定期的にあちこちで話題になる確率の問題です。
調べると2chまとめサイトなどでも話題にされていますし、考察しているブログなども多数見つかります。
Yahoo!知恵袋では早稲田大学の過去問だという方がいました。
論調もいろいろで、1/4だよ派と10/49だよ派だけに限らず、本文の解釈の仕方で違うだの、この問題は単純な確率の問題ではないだのと様々な意見が出されています。
実際には数学的にきちんと議論できて正解も出せるのですが、それでは納得できない人は大勢います。数式で考えるというのは抽象化のレベルが相当高いので、計算上はともかく問題文を本当に反映できているのか?という疑問が起きるのは不思議なことではありません。
あれこれ議論する前に、実際にやってみればいいんですね。
今回はその結果の話と、結果の「正しさ」の扱いについて少し書いておきます。
「抜き打ちテストのパラドックス」という有名なパラドックスがあるのですが、たいていどの記事でもパラドックスの紹介だけで終わっていて、もやもやするのでこの記事を書きました。
自分の中ではパラドックスのありかがわかっているつもりなのですが、同意見の主張が見つからないので多少気になっているところでもあります。
Taken by fdecomite, Flickr
抜き打ちテストのパラドックスというのは、以下のようなものです。
「とある学校、とあるクラスの話。あるとき先生が以下のように言いました。
『来週の月曜から金曜の間に、抜き打ちテストを行います。ただし、君たちはこの抜き打ちテストがいつ行われるか予測できない。』
「サンクトペテルブルグのパラドックス」は、現実的にはあまり儲からなそうな賭けの期待値が、計算上無限大に発散するとされる有名なパラドックスです。
パラドックスを知らない人のために賭けの要点を書いておくと、以下のようになります。
「コインを投げ続け、表が出たらゲーム終了。表が出たのが1回目なら1円獲得、2回目なら2円、3回目なら4円…というように、裏が1回出るたびにもらえる金額が倍になる。いくらの賭け金ならこの賭けに参加するべきか。」
儲け額の期待値Wは以下のように計算されます。1/2で1円、1/4で2円、となるので…
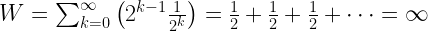
ここまで見てだまされないぞと思った人は、しっかり悩んでみてください。
Taken by xJason.Rogersx, Flicker.
先日友人との間で話題になって、実際のところおおよそどんな具合で儲かるのかやってみようということでさくっと書いてみたものです。確率についてなんやかんやと議論するのも楽しいですが、ゴリ押しでデータを集めるのもまた面白いものがあります。あと探しても意外とそういう資料が見当たらなかったので。
いつもどおりC++です。C++11の機能を使っていますので、例えばgccとかでコンパイルしたい場合は -std=++11 とか -std=c++0x とかのオプションをつけてください。
#include <ctime>
#include <iostream>
#include <random>
#include <functional>
int main(int argc, char** argv){
if(argc != 2){
std::cerr << "Wrong argument!" << std::endl;
return -1;
}
long long int loopNum = 1;
for(int i = 0; i < atoi(argv[1]); i++){
loopNum *= 2;
}
std::cout << "Loop: " << loopNum << std::endl;
time_t timer;
time(&timer);
auto rand = std::bind(std::uniform_int_distribution(0,1),
std::mt19937(static_cast<unsigned int>(timer)));
long long int total = 0;
for(long long int trial = 0; trial < loopNum; trial++){
long long int earn = 1;
while(rand()){
earn*= 2;
}
total += earn;
}
std::cout << "Earned: "
<< static_cast<double>(total)/static_cast<double>(loopNum)
<< std::endl;
return 0;
}
特記するようなものもありません。コマンドライン引数から2の何乗回計算するかを決めて、律儀に試行を繰り返して平均獲得金額を求めています。
カウントがlong long int型なので2の50乗回程度までは問題ないと思いますが、そのはるか手前の2の30乗前後(数億程度)で計算時間がきつくなってくると思います。
まあ乱数も毎回1ビットしか使っていないしシングルスレッドだしで、高速化する余地はまだ残っています。
大量に試行した結果は以下のようになります。あくまで愚直に。力強く。
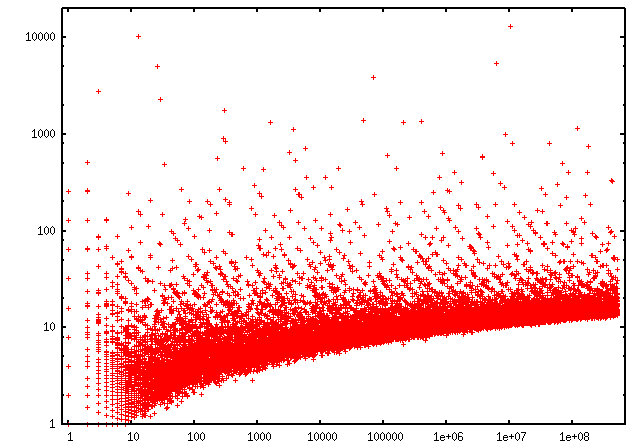
横が1セットあたりの試行回数、縦が1回あたりの平均獲得金額です。両方logスケールなのに注意。
(表が出るまでを1回の賭けとし、1セットでn回行うと定義しています。平均獲得金額は儲け額をnで割った値。)
不思議なグラフです。まず、回数を増やすと平均獲得金額は順調に上がっていくことがわかります。1,000,000,000回以上やるつもりなら、1回あたり10円以上儲かることがほぼ確実になります。このままグラフを右に伸ばしていったらどうなるでしょう。
もうひとつ面白いことがあって、それはばらつきが減らないことです。例えば右上にある点、だいたい10,000,000回で平均獲得金額が10,000円を超えていますが、つまりこの1セットで単純にトータル一千億円以上儲けているということです。とんでもない大当たりです。
胴元と挑戦者、どちらの席につきたいですか?
今回は横軸がlogスケールで均等になるようにサンプリングしています。離散的な値しかとらないので左側はすかすかに見えますが、実際は点が重なっているだけです。
また、左上から右下へのぼんやりとした斜線が大量に見られます。これは「1回大当たり」を成し遂げたときの線になっています。回数を増やすと同じ大当たりでも「1回あたりの獲得金額」は減っていくので右下がりになるという具合です。その代わり「もっとすごい大当たり」をひく確率も出てきます。
モンテカルロ法などでは試行回数を増やすと値が落ち着くのですが、この問題はおもしろいことにいくら試行回数を増やしてもばらつきが収まらないようになっています。よくできています。
儲け額の分散も出してみようと一度書きかけたのですが、ちょっと考えてからこの問題に対して無駄な試みであることがわかりました。
コンピュータはしばしば想像力を働かせる道具として役に立つのですが、今回のように神通力の効かないヤバそうな問題ではちょっとわけが違ってきます。こんな問題でも扱えてしまう数学の力は偉大です。
結果の意味とこの賭けの本当の期待値についてはいろいろ考えてみて下さい。
確率の分野でとても有名な問題のひとつの表現です．確率の入門書に限らず，この手のパズルを紹介する書物などでもよく見かけ，またインターネット上の様々なコミュニティで定期的に話題になります．
Yahoo!知恵袋でも検索をかけると数十件程度同じ内容の質問が並んでいたりします．テレビ番組で取り上げられたこともあるようですね．
なんやかんやと炎上したあげく，答えは1/3だという結論に達するのが定番の流れです．
私はこの問題，いつも間違ってるんじゃないか?と思っています．少なくとも問題文に矛盾があって，答えを1/3とするのは乱暴すぎるような気がしています．
まず挙げられる(間違いとされる)答えは
「性別なんてもう片方の性別には関係していない．だから1/2だ」
というものです．これに対する反論はだいたい以下のようになります．
「想定されるパターンは(男，男)，(男，女)，(女，男)，(女，女)の4種類である．このうち4番目は問題文より除外されるので，残り3パターンから考えて1/3だ」
この説明は一見正しそうに見えます．ただ，上の説明で問題文の「もう1人が男」を考えるとどうにも不穏な空気が漂い始めます．特に(男，男)のときのもう1人ってどっちでしょう?
問題文を見てみると，問題文前半では単に「1人は～である」という表現が使われているだけです．これは(答えを1/3とする文脈では)「～という人が1人以上いる」と言っているだけであり，特定の人のことは何も記述していません．じゃあその後に続く「もう1人」は?と考えると，そんなものは定義できないことがわかります．
(問題文のつじつまをあわせるなら，「1人は男である」を特定の人にすることになり，答えは1/2になるでしょう．この場合は上の誤答とされていた表現もすんなりくると思います．)
この記述のおかしさは男女というどちらも起こりそうな現象で考えると気づきにくいですが，もっと確率の偏った出来事に置き換えて書けば雰囲気が変わります．
「太陽と月のうち少なくとも片方は東から出て西に沈む．もう片方は～」
と書くと，いやいや，もう片方なんてないでしょう，となると思います．(前半の文には特に間違いはありません．)
出題者の意向通り答えを1/3としたいなら，問題文は「両方男である確率は?」としないとおかしくなります．細かい違いのようですが意味が全然変わってきます．
以前Slashdotに載った記事で「子供が二人いて、(少なくとも) 一人は火曜日生まれの男の子である。もう一人の子供も男の子である確率は ?」という問題を扱うものがありました．
問題の原文は “I have two children, one of whom is a son born on a Tuesday. What is the probability that I have two boys?” となっており，問題はなさそうです．
ところが英語版の記事に転載された段階で “What’s the probability that my other child is a boy?“となってしまい，ここから変な話が始まってしまっています．
(ちなみに原文での答えは13/27になります．これは火曜日という一見どうでもよさそうな条件が答えに影響するという点に面白さがある，と紹介されています．考えてみて下さい．)
まあこんなのは言葉遊びだと言われればそうかもしれませんが，一度問題を正しく把握してしまえばあとは適当な手段で計算するだけなのであって，その段階に落としこむまでのほうが大事であることはよくあることではないかと思います．
私が一番気になったのは，こういう質問に答える側の人があまりこういう議論(問題文に矛盾がある，とか)をしないのだなと思ったことです．元が有名な問題なのでたぶんどこかで聞いた/議論した答えを輸入しているのだと思いますが，もし正しい答えとされるものを十分な吟味なしに「正しい答え」として広めているのであれば，それは自分の出した答えが間違っている以上に危険なことではないかと私は思います．