全体は部分の総和に勝る。 – アリストテレス
マンデルブロー集合、10の200乗倍、グーゴル倍のグーゴル倍に挑戦しました。
Youtubeのほう、最後がぶつ切りになってしまっていますが許してください。
ニコニコ動画はこちら。
(追記)もっと画質のよい動画が欲しい場合はGoogle Driveからダウンロードして下さい。1GB弱あります。
現実世界だと陽子や電子の半径が10の-15乗メートル、観測可能な宇宙の範囲でもたったの(?)10の27乗メートルしかないため、これほどの倍率はまず見かけることはありません。
ニコニコ動画で何度も見返した動画というのはそれほど多くないのですが、その一つに「【超高倍率】マンデルブロー集合【10の100乗倍】 (hoho様)」というものがあります。今回はその動画に感謝しつつ、記録更新を狙いました。
先の動画ではニコニコ最高記録と記されているので、それが正しければ今回がニコニコ新記録です。(logスケールで)一気に2倍まで来たことになります。
続編はこちら: マンデルブロー集合へ飛び込む
マンデルブロー集合の定義と性質・色のつけ方
マンデルブロー集合 (Mandelblot Set) というのは複素数の集合です。定義は「0からはじめて、2乗して複素数Cを足す動作を延々行ったときに値が収束するようなCの集まり」です。
数式で表すと以下のようになります。
このzが発散しないCを集めたものがマンデルブロー集合です。例えばC=1なら発散するので集合の要素でない、C=-1なら収束するので集合の要素、という具合です。
複素平面で表示すると以下のようになります。
雪だるまみたいですね。
この画像はウィキメディア・コモンズからの転載ですが、他にも様々なマンデルブロー集合の映像がありますが、綺麗なのでぜひご覧になって下さい。
この集合のおもしろいところは、何よりもまずフラクタルであることです。つまり、表面のでこぼこには限界がなく、拡大していくと無限にでこぼこが繰り返されていきます。
飛び地のように見える箇所は実際にはすべてつながっていることが示されています。
さらに、周辺の領域に対して発散する速さに応じて色をつけることで不思議な模様があらわれます。
発散する速さというのは、例えばzがある範囲を超えたときの計算回数nによって決めることができます。zの絶対値が2を超えると発散することがわかっているので、今回はそれを指標にしています。
この模様は「足して2乗を繰り返す」という単純な数式から出現するとは思えない摩訶不思議な雰囲気を漂わせていて、特にフラクタル独特のスケール感の無さ、つかみどころの無さも相まって多くの人を魅了してきました。そのため「神の指紋」などと呼ばれることもあります。
実装について
さて、数学の上でこそ「無限に繰り返す」と表現することができますが、いざそれを本当に描画しようと思うと話は別です。
微小な領域を拡大するほど収束と発散の境は微妙になり、2乗を繰り返すにしても桁打ち切りの計算誤差がどんどん大きくなっていくため、まともに計算したのではすぐに限界がきてしまいます。
はやい話がC言語のfloat型とかdouble型ではとても太刀打ちできないわけです。そこで任意精度演算の実装が必要になります。今回使ったGMP (The GNU Multiple Precision Arithmetic Library) などは有名どころです。
(以前GMPを導入したのはこういうことをするのが目的でした。当然今までに行なってきたようなシミュレーションでも高精度な計算をするに越したことはないのですが、よほどの事情がない限り科学技術計算でもdouble型を使うことでおおよそ十分な精度としています。)
もちろん必要になる計算時間も拡大するほどざくざく増えていきます。先ほどの動画では10の100乗倍まで拡大したものですが、はじめて見たときには「コンピュータでここまで描けるのか!」と感動したものです。
今回はその感動した昔の自分自身への挑戦として、10の200乗倍までの拡大を試みました。
マルチプロセス並列化を行なっていますが、CPU時間でおおよそ200時間程度かかっていると思います。それでもコンピュータの進歩とはすごいものです。拡大するエリアによって模様が大きく変化するため別の地点を狙ってもよかったのですが、場所ごとに計算時間が全然異なる(例えば集合から遠いところは一瞬で計算できる)ため、先の動画でのターゲットと同じ場所とさせてもらいました。他の地点も後でちょっと見てみたいですね。
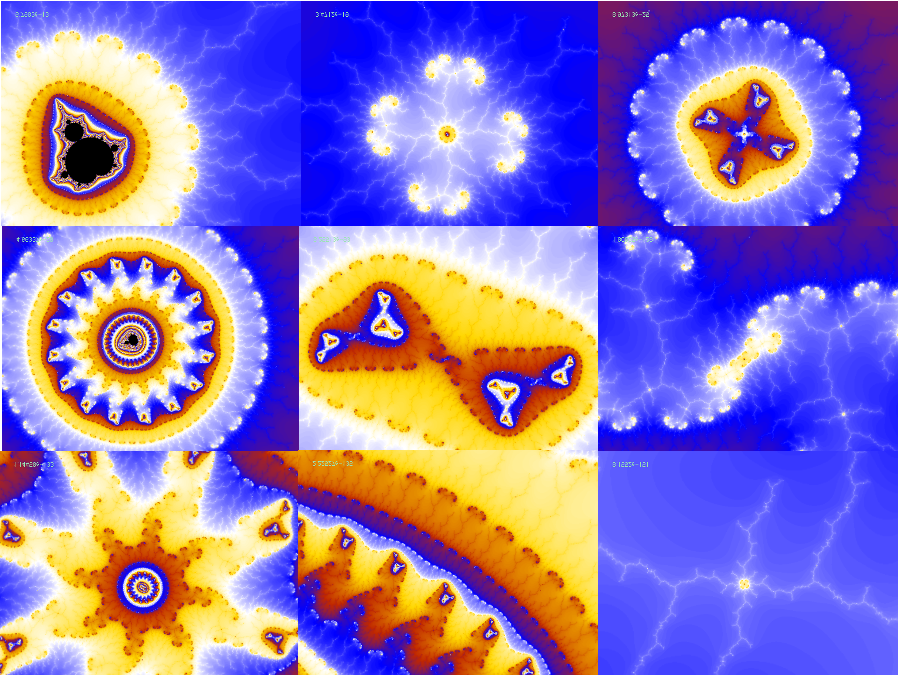
動画のスナップショットを何枚か。
100乗以降の前半はフラクタルらしさの現れる場所、後半は賑やかな模様を狙って拡大しています。
次回はソースコード周りの説明と、他の場所の写真集(?)も用意できたらと思います。
10の100乗倍というネタと楽しい拡大地点を紹介して頂いたhoho様、ありがとうございました。


ピンバック: 最近のブログ記事まとめ | ぞうさんの何でもノート
ピンバック: マンデルブロー集合へ飛び込む | ぞうさんの何でもノート