[作ってみた] [プログラミング] 剛体3重振り子

以前ここで書きかけた剛体振り子のプログラムですが、いろいろと紛失してしまったので新しく作りました。

ソフトのダウンロードはこちらから pendulums

ソースコードはgithubからどうぞ https://github.com/So-Takamoto/triple_pendulums/
手元の環境はVisual Studio 2010です。

例によってC++, OpenGL+freeglutで作成しています。
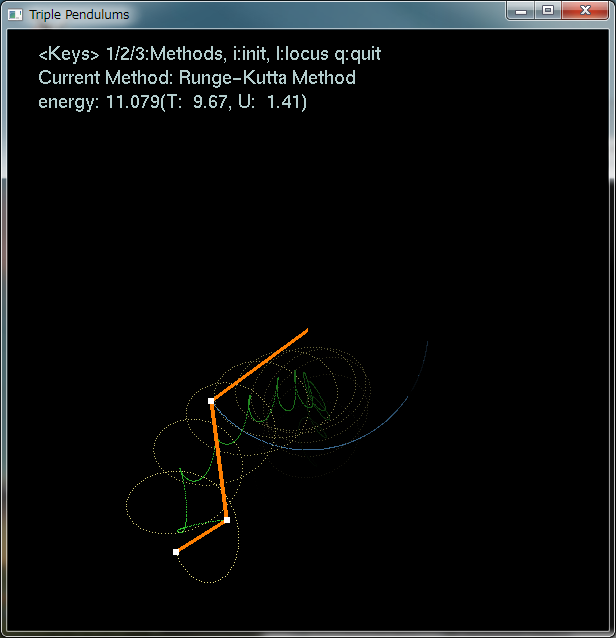
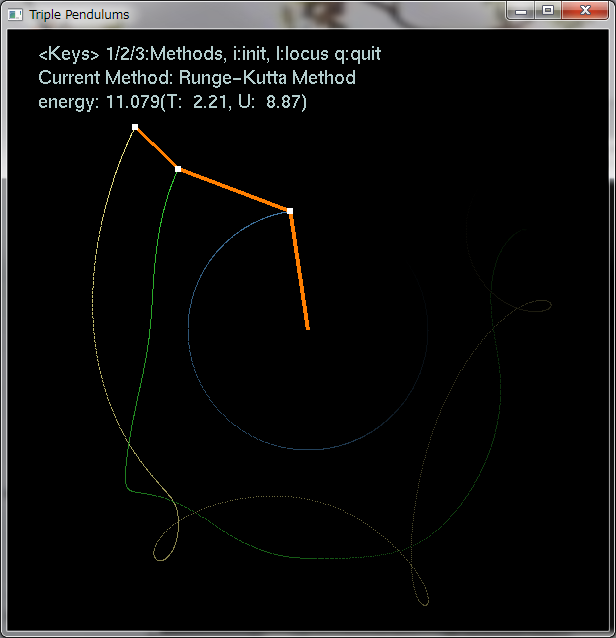
キーの1,2,3で微分方程式を解く方法を変更でき、iで初期化、lで軌跡の表示切り替え、qで終了です。

質量や重力加速度、初期条件、各振り子の長さを変えたい場合はソースコードをいじってみてください。
64bit版でコンパイルを行いたい場合はfreeglutのライブラリを64bit版に変更してください。今回は軽いのであまり必要はないかと思いますが。

例によって動画を用意しておきます。

なんでこんなシミュレーションをしようと思ったかの話は以前書いた(早い話がこういうおもちゃが大学に置いてあった)ので、今回は原理とか内容の紹介メインにしたいと思います。

今回扱う系は平面上の棒3個なので、そのままで言えば3自由度×3個=9自由度の系なのですが、各ジョイントが2自由度分の拘束を持つため結局本来の自由度は3になります。

ひとつのやり方は、これらのジョイントにかかる力を陽に扱う方法です。利点は自由度を実座標と対応付けられるため意味がわかりやすいことと、比較的機械的な処理で立式できることです。
これらジョイントにかかる力は幾何学的な関係から導出することもできますし、今回のような単純なリンク機構であればエンドエフェクタ(一番先の振り子)から芋づる式に数値解析の範囲で導出することもできます。ロボットハンドなどの制御ではこの辺りの話が動力学計算としてたくさん出てきます。

一方で今回のような系ならそこまで面倒な話をしなくても、解析的に運動方程式を求めることができます。こういう系ではラグランジュ形式を出発点にすると便利です。ジョイントに働く力を陽に扱わずに、自由度の数だけ運動方程式を考えればいいからです。

ラグランジュの運動方程式の出発点は、ラグランジアンL(=T-U)の表現です。運動エネルギーTは重心の並進運動と回転運動から、位置エネルギーUは重心の位置から求まります。

3つの剛体を根本から順に0,1,2と置いて(0から始めるのはC言語使いの癖です)、それぞれ棒の角度を $\theta_{i}$ 、長さを $l_{i}$ 、質量を $m_{i}$ 、根元側のジョイントからの重心の相対位置を ${\bf x}_{ri}$ と置きます。3自由度はここでは3つのθに対応します。

このとき、相対位置と相対速度について、

${\bf x}_{ri} = (\frac{1}{2}l_{i}\sin{\theta_{i}},\frac{1}{2}l_{i}\cos \theta_{i})\\ {\bf v}_{ri} = \frac{\partial}{\partial t}{\bf x}_{ri} = (\frac{1}{2}l_{i}\dot{\theta}\cos{\theta_{i}},-\frac{1}{2}l_{i}\dot{\theta}\sin{\theta_{i}})$

また、絶対位置 ${\bf x}_{i}$ について、

${\bf x}_{0}={\bf x}_{r0}\\ {\bf x}_{1}=2{\bf x}_{r0}+{\bf x}_{r1}\\ {\bf x}_{2}=2{\bf x}_{r0}+2{\bf x}_{r1}+{\bf x}_{r2}$

速度 ${\bf v}_{i}$ も上式を微分するだけです。欲しいのは $\frac{1}{2}m_{i}|{\bf v}_{i}|^{2}=\frac{1}{2}m_{i}{\bf v}\cdot{\bf v}$ なので、展開して内積を計算すればそれぞれ導出できます。

回転のエネルギーについては $\dot{\theta}$ と慣性モーメントから計算できます。長さlの棒の慣性モーメントIは $I=\frac{1}{12}ml^2$ なので、回転のエネルギーについては $\frac{1}{24}ml^2\dot{\theta}^2$ と求まります。

なんやかんやで計算すると以下のようになります。

$T=(\frac{1}{6}m_{0}+\frac{1}{2}m_{1}+\frac{1}{2}m_{2})l_0^2\dot{\theta_0}^2\\ +(\frac{1}{6}m_{1}+\frac{1}{2}m_{2})l_1^2\dot{\theta_1}^2\\ +(\frac{1}{6}m_{2})l_2^2\dot{\theta_2}^2\\ +(\frac{1}{2}m_{1}+m_{2})l_0l_1\dot{\theta_0}\dot{\theta_1}\cos(\theta_0-\theta_1)\\ +(\frac{1}{2}m_{2})l_0l_2\dot{\theta_0}\dot{\theta_2}\cos(\theta_0-\theta_2)\\ +(\frac{1}{2}m_{2})l_0l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)$

汚いようですがθに関しては対称的な形をしています。

同様に位置エネルギーに関しても

$U=(\frac{1}{2}m_0+m_1+m_2)gl_0\cos\theta_0+(\frac{1}{2}m_1+m_2)gl_1\cos\theta_1+(\frac{1}{2}m_2)gl_2\cos\theta_2$

ラグランジアンLは先に書いたようにL=T-Uとして求まります。あとはラグランジュの運動方程式

$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_i}}-\frac{\partial L}{\partial \theta_i}=0$

を解けば $\ddot{\theta_i}$ について求まるという算段です。ただし、上の式を解こうとすると $\ddot{\theta_i}$ についての3元連立方程式になるので、微分方程式を解く前に適当な方法で変数を独立させておく必要があります。3変数なら一応解析的にも書き下すことができますが、大変面倒なので今回はガウス・ジョルダンの消去法を使いました。

ラグランジュ形式は便利ですが、最後に出てくる式がいまいち意味付けしにくいという不思議なところがあります。もっとも世の中の物理というのは別に人間にわかってもらうために運動しているわけではないのですが。
そもそもラグランジアンL自体なんの値なのかと考えだすと悩みどころはどんどん増えていきます。教科書には「意味のある値ではない」ときっぱり書いてあったりします。清々しいですね。

まあそれでもハミルトン形式まで持っていけばハミルトニアンHに意味を持たせることができるのですが。

運動方程式が解けたら次は微分方程式の数値計算の出番です。

微分方程式を数値計算で解く方法は数多くあります。今回のプログラムでは3種類から選べるようにしています。すべて陽解法で、それぞれ1次、2次、4次の精度を持っています。

おそらく最もシンプルでわかりやすい方法がオイラー法で、離散化した点の間を直線で補間する方法です。直線なので1次の精度がある、と表現されます。
オイラー法は精度が悪いため一般には使われません。左上のエネルギーの値のぶれが大きいことからもわかると思います。

より高い次数まで精度を持たせた方法があり、例えば4次のルンゲ・クッタ法が有名です。今回は2次のホイン法も用意しました。エネルギーの値を見れば違いがわかると思います。

ただし、たとえ4次精度を持っていたとしても長期間のシミュレーションを行うと次第にエネルギーが変化していってしまいます。長期間のシミュレーションでこういう性質があると結構問題で、例えば太陽系のシミュレーションをしていたら計算誤差で惑星が吹っ飛んでいったとか、分子の運動をシミュレーションしていたら計算誤差で勝手に沸騰した、なんていうよくわからないことが起きてしまいます。こういう場合にはエネルギーが長期間で安定するよう工夫した数値計算を行う必要があります。シンプレクティック性を持つ計算などと呼ばれますが、いちいち書いていたらとんでもない量になるのでここでは割愛します。

私の研究分野でよく使われる速度ベルレ法などの計算手法はうまい具合にこのシンプレクティック性を持っており、2次精度の手法ですが、計算が簡便でしかも陽解法でありながら長期間でエネルギーが変化しにくいという便利な性質を持っています。

系としてはとっても単純でありながら、運動はとても不規則です。時には大きくゆったり回ったり、時には先の振り子だけぐるぐる回ったり、それらを予告なく切り替え続けます。

このような運動はカオスと呼ばれますが、単純な法則から複雑な運動が生まれる例は他にもたくさんあって、例えば前回の反応拡散系も支配している方程式は単純ながら模様が複雑になったりもします。

それなら逆に、世の中の一見複雑な現象も実は単純な法則によって成り立っているのではないか?と考えるものの見方があります。では複雑な運動から単純な法則は見つけることができるのか?振り子ではなく、例えば世の中の気候の変化、株価、人の行動のような複雑な現象は実は単純な法則から成り立っているのではないか?そうだとしたらその法則は何か?という疑問に答えるのが、「複雑系」と呼ばれる学問のひとつの目標なのではないか、と私は勝手に考えています。

まあ、私は複雑系の研究者ではないので、好き勝手に妄想しているところが大きいのですが。

ぞうさんの何でもノート

思いついたことを書いていきます

[作ってみた] [プログラミング] 剛体3重振り子

「[作ってみた] [プログラミング] 剛体3重振り子」への3件のフィードバック

コメントを残すコメントをキャンセル

「[作ってみた] [プログラミング] 剛体3重振り子」への3件のフィードバック

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル