前々回の振り子の欄でちょっと触れた運動方程式の数値計算の話の続きです。
運動方程式は立てるだけでなく、実際に方程式を解かないとシミュレーションは行えません。
一番丁寧な運動方程式の解き方は解析的に解くことですが、ほとんどの場合うまい方法がないことがわかっています。例えばN体に万有引力が働いて運動する系ではNが3以上になると解析的に解けなくなることが知られています。太陽と地球と月でもうオーバーです。
もっと一般的に扱いたいときは、コンピュータが強力な武器になります。微分方程式を差分方程式に近似してしまえば計算機で簡単に扱えるので、後は時間の刻み幅を十分に小さくとってあげれば微分方程式に近い解が得られるというわけです。
じゃあそれで話は終わりかというとそうでもなく、この差分方程式にする段階がなかなかうまくいかないわけです。それに伴っていろいろな手法が提案されています。今回はその話です。
今回作ったものは互いに引力を及ぼし合う粒子たちのシミュレーションです。
イメージしているのは銀河系的なアレですが、まあ数値積分の例で作っただけなので本気で似せているわけではありません。私は中学校で習う電子の描像のイメージに似ているなと思いました。
IAEAのマークにもあるアレです。
中央に質量の大きめな粒子をひとつ、あとは小さな粒子をばら撒いています。小さな粒子同士も相互作用します。
大事なのはこの系では力学的エネルギー・運動量・角運動量が保存するということです。シミュレーションでエネルギーが保存していなかったら、それは何かおかしいことが起こっているぞ、というわけです。
可視化の部分は振り子の流用ですね。数字キーでシミュレーション手法を変えたり、初期化したり軌跡のオンオフを行ったりします。
後述するオイラー法、ホイン法、ルンゲ・クッタ法、速度ベルレ法を実装しています。
いつものようにプログラム: particle
ソースコード: GitHub
微分方程式を解く際、おそらく最も単純な差分化はオイラー法です。
ニュートンの運動方程式は2階の微分方程式ですが、速度v自体も変数と置いてしまうことで1階の微分方程式に置き換えることができます。以下の式で左辺をx、右辺をfと置いてしまえばいいわけですね。
オイラー法では以下のような差分化を行います。⊿tは十分に短い時間をとります。
見た目にわかりやすいため学習用として頻繁に登場しますが、正確なシミュレーションをしたい場合向きではありません。誤差がとても大きいからです。
誤差が大きい理由は2点の補間を直線、つまり1次式近似にしているからで、それなら2次や3次の項を追加して補間しようというアイデアがあります。実際これはうまく行きます。
よく使われるものに4次多項式で補間するルンゲ・クッタ法というのがあります。
tからt+⊿tまでの4点で傾きを計算して、適当に混ぜることで4次の精度を出しています。式中の諸係数を求めるのにはそこそこの手間がかかります。
次数を上げるほど多項式補間の精度は上がりますが、そうすると計算の安定性の議論から時間刻み⊿tをかなり小さくとらないといけなくなってしまうこと、また計算コストが上がるのでそれなら次数を上げずに時間刻みを減らしたほうが都合がいい場合が多いことなどがあり、結果としてこの4次のルンゲ・クッタ法はよく使われます。
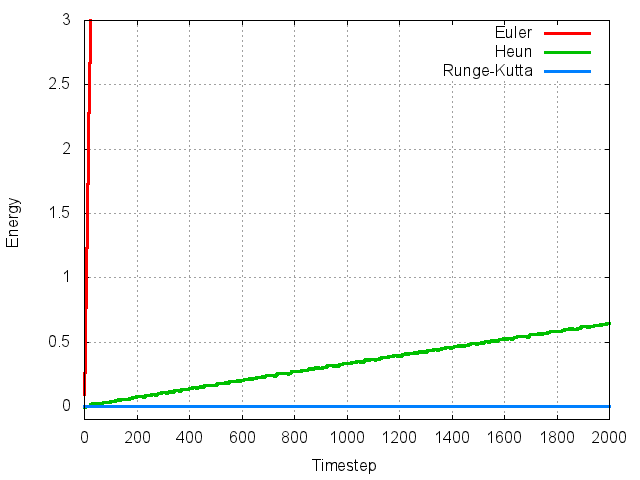
1次、2次、4次の各手法で時間経過とエネルギーのずれをプロットしたものが以下になります。
1次のオイラー法は目に見えて粒子が遠ざかっていってしまいます。2次(ホイン法)と4次(ルンゲ・クッタ法)はシミュレーション結果を見た雰囲気では似ているものの、エネルギーを見るとホイン法はだんだんとずれていくことがわかります。
もちろんオイラー法にも利点はあって、軽くて実装が楽なので、正確さにあまりこだわりがない場合にはいちばん手軽な解法になります。
陰的解法と言われる手法群もあるのですが、一般に複雑なので今回は省略します。
速度ベルレ法
ここで、今回メインで書きたかった手法「速度ベルレ法」を紹介したいと思います。2次の精度をもつ手法です。
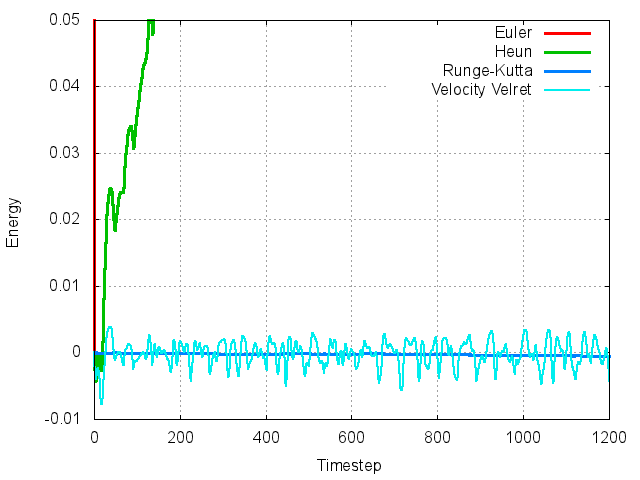
2次ならルンゲ・クッタ法より精度が悪いのかというとそうでもありません。先のグラフの倍率を上げたものに速度ベルレ法を追加してみます。
ルンゲ・クッタ法に対してぶれは大きいですが、ホイン法のようにエネルギーが変化していくことはありません。しかしまだこれではルンゲ・クッタ法のほうが頼りがいがあるように見えます。
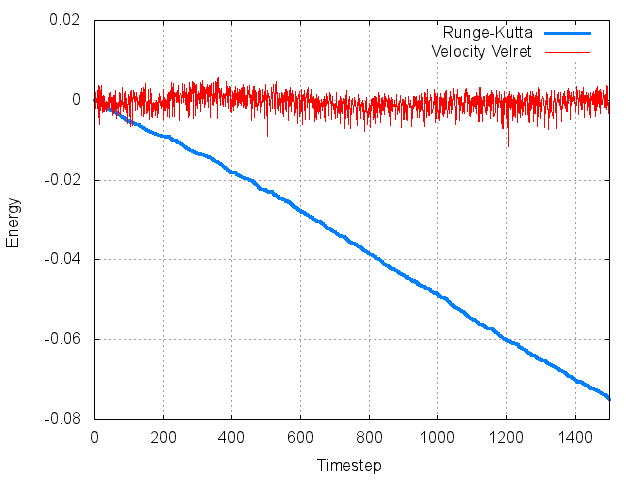
面白いのは長時間の振る舞いです。このまま横軸のスケールを100倍にしてみます。
ルンゲ・クッタ法もこの長時間では計算誤差が積もってエネルギーがずれていくのに対して、速度ベルレ法はほぼ初期の振る舞いを保ったままとなっています。短期間のぶれは大きいのに、長期間でずれていかない不思議なグラフになっています。
速度ベルレ法の式は以下のようになります。位置と速度を分けて扱うのが今までの手法と違います。
なぜこのような振る舞いを見せるのかにはわけがあって、この速度ベルレ法はシンプレクティック性というとても重要な性質を持つように作られています。
ここからちょっと難しい話ですが、ニュートンの運動方程式は時代を追ってラグランジュ形式、ハミルトン形式へと再公式化されていきます。このハミルトン形式で表現したとき、運動は位相空間上で体積を保つ性質があることがわかっています。
速度ベルレ法も含まれるシンプレクティック積分法と呼ばれる手法では、この位相空間での体積を保存する性質を有していて、結果的に長時間でのシミュレーションで(ある種の)誤差が積もっていく現象が起きなくなっています。
ハミルトン形式におけるとある保存量を厳密に保存しており、時間反転対称性(終了状態から反対向きにシミュレーションを行うと開始状態に行くことができる)、エネルギーなどの保存量を保存する、といった今までの手法にはなかった性質があります。
速度ベルレ法は、私が研究でよく扱う分子動力学法でもよく使われています。系を長時間観察するときなどにこの性質がとても有効だからです。また分子動力学法では計算コストのネックが力の計算になっており、1回に多段で力の計算を行うルンゲ・クッタ法などは相性があまりよくありません。
式自体は単純なため「分子動力学法で使われる数値計算は単純」という表現をよく耳にします。しかしその構成はよく考えられていて、裏側には先人の知恵がたっぷり詰まっていることは確かです。
運動方程式ひとつをとっても様々な数値計算法がありますが、どの積分法が正しいかといった議論はあまり有益ではなく、私のイメージでは「どれも間違っているが、間違え方が違うので場合に応じてどうしても譲れないものに応じて選ぶのが良い」としか言えないかなと思っています。
例えばゲームの物理演算などでは、そこらへんの物が綺麗な放物線を描かなくてもそんなに気になりませんが、プルプル震えたり突然とんでもない勢いで吹っ飛んでいったりすると見た目からしてヤバい、ということになるわけです。それなら計算精度より安定性と計算コストを重視しようとなるわけです。
では、現実のこの世界は、どんな手法で運動方程式が解かれているのでしょう。これはちょっと危険な問いで、そもそも現実世界が運動方程式に厳密に従っているのか、宇宙は連続体なのか、シミュレーション可能なのか、といったことからあれこれ考えなければいけません。
まあでも、私が宇宙をひとつ作っていいと言われたら、たぶんオイラー法を採用します。一番単純だし、世界がそんなに複雑な式でできているとは考えたくないからです。
後半では、今回のシミュレーションで作った系について(なぜ前回の振り子のままではだめだったのか、星の運動としてこの動きの胡散臭さは何か、ソースコード云々)の説明をしたいと思います。
速度ベルレ法と言っても万能ではないのです。

ピンバック: 運動方程式の数値計算と速度ベルレ法の威力 (後半) | ぞうさんの何でもノート
ピンバック: 最近のブログ記事まとめ | ぞうさんの何でもノート
ピンバック: [フラクタル] マンデルブロー集合 10の200乗倍への挑戦 | ぞうさんの何でもノート